Visualizing the Birman-Series Set on the Punctured Torus
Faculty mentor: Nicholas Vlamis
Grad student mentor: Mark Greenfield
Undergraduate researchers: Connor Davis, Ben Gould, Luke Kiernan
Birman-Series showed that the union of all simple closed geodesics on a hyperbolic surface has Hausdorff dimension 1; in particular, they take up very little room on the surface. This was quantified by the work of Buser-Parlier, where they showed that given a hyperbolic surface there exists an embedded hyperbolic disk that no simple closed geodesic enters, where the radius depends only on the topology of the surface (not the geometry!). The goal of this project is to visualize the union of the simple closed geodesics on hyperbolic punctured tori at different points in moduli space.
Here is the poster describing the project in more detail.

Pictured above on the left is the union of the first 600 closed geodesics (up to word length) followed on the right by the union of first 100 simple closed geodesics (up to word length) in a fundamental domain in the hyperbolic plane for a once-punctured torus. These images were drawn by the students using a program they wrote using the language Sage. The code can be downloaded here. The program includes an interactive GUI allowing the user to set the number of geodesics pictured as well as to move through a 1-parameter family of hyperbolic structures.
Billiards and Dynamics
Faculty mentors: Sandrine Daurat and Diana Hubbard
Grad student mentor: Jasmine Powell
Undergraduate researchers: Amanda Burcroff, Wenyu Jin, Max Kontorovich
This project investigates dynamics from the point of view of billiards. We will explore billiards on a number of different domains, both in the plane and in higher dimensions, focusing on how the behavior of trajectories change as we vary certain parameters of the tables. These explorations take place both mathematically, touching on topics from symplectic geometry, topology, and physics, as well as visually. One project objective is to design interactive simulations of billiards for other students to use for their own experimentation.
Below are some visualizations and simulations produced for this project.
 This is an unfolding of a billiard orbit on an irregular polygon. This method can be used to show that the Hausdorff dimension of the phase space of an open polygonal billiard table is always 1 or 0.
This is an unfolding of a billiard orbit on an irregular polygon. This method can be used to show that the Hausdorff dimension of the phase space of an open polygonal billiard table is always 1 or 0.  A classical billiard orbit in a 3D ellipsoid. When projected onto any of the three standard coordinate planes, this orbit coincides with a billiard orbit on the 2D ellipse.
A classical billiard orbit in a 3D ellipsoid. When projected onto any of the three standard coordinate planes, this orbit coincides with a billiard orbit on the 2D ellipse.
Some simulations of billiard dynamics created by the students using Geogebra are available at the following links: Unfolding an Irregular Hexagon, Billiards on any Conic, Billiards on Ellipse with Midpoints, Billiards on Ellipse.
Visualizing Convex Projective Surfaces
Faculty mentors: Caleb Ashley, Anton Lukyanenko
Grad student mentor: Feng Zhu
Undergraduate researchers: Samuel Freedman, Jacob Shulkin, Eric Winsor
Any finite-type surface with sufficient genus and/or punctures can be given a convex projective structure: an atlas of coordinate charts which gives the surface, locally, the geometry of real projective space. In a 1990 paper, W. Goldman described explicit coordinates for moduli spaces of such structures. Some of these coordinates come from hyperbolic geometry and are fairly well-understood: they correspond to lengths of certain curves, or twists about them; however, the other coordinates remain somewhat mysterious. This project aims to explore and create visualizations of these structures, in an attempt to better understand Goldman’s coordinates.
Here is the poster describing the project in more detail. Below are some of the visualizations produced during the project.
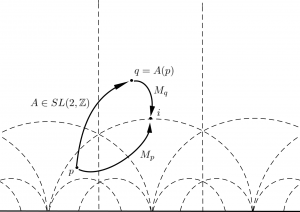
Above is a schematic illustration of “incidental rotation” in the SL(2,Z) action on lattices.
This shows a projective deformation of a degenerate pair of pants, seen from the universal cover(s). Click on the image above to see the animation.